“Convex optimization”

凸优化（convex optimization）是最优化问题中非常重要的一类，对于机器学习来说，如果要优化的问题被证明是凸优化问题，则说明此问题可以被比较好的解决。

梯度下降法

梯度下降法(Gradient descent)或最速下降法(steepest descent)是求解无约束最优化问题的一种常用的、实现简单的方法。

梯度

多元函数是一个平面，方向有很多，可以通过方向导数来表述任意方向的导数。

assume: 二次函数 f(x,y) 方向u=cosθi+sinθj(单位向量)，方向导数公式如下：

$D_{u}f$ = $\lim _{t\rightarrow 0}\dfrac {f\left( x+t\cos \theta ,y+t\sin \theta \right) -f\left( x,y\right) }{t}$

= $f_{x}\left( x,y\right) \cos \theta +f_{y}\left( x,y\right) \sin \theta$

= $\begin{bmatrix} f_{x}\left( x,y\right) & f_{y}\left( x,y\right) \end{bmatrix}$ $\begin{bmatrix} \cos \theta \\ \sin \theta \end{bmatrix}$

=A*I

cosα

其中α是两向量的夹角，为0时方向导数达到最大，此时方向导数即为梯度。

梯度下降算法

算法调优

步长选择
参数初始值选择：初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值，当然如果损失函数是凸函数则一定是最优解
归一化：由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化

BGD、SGD、MBGD

批量梯度下降法（Batch Gradient Descent）：在更新参数时使用所有的样本来进行更新
随机梯度下降法（Stochastic Gradient Descent）：仅选取一个样本来求梯度
小批量梯度下降法（Mini-batch Gradient Descent）：小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于 m个样本，我们采用x 个样子来迭代，1<x<m。一般可以取 x=16,32,64…,可根据样本数据调整。

牛顿法

牛顿法主要应用在两个方面，1：求方程的根；2：最优化

–>前置知识：

Hesse Matrix

海塞矩阵是二阶偏导数方阵，描述了局部的曲率函数,对于一个多元函数 f(x1,x2,…xn) ,如果它的二阶偏倒都存在，则海塞矩阵可以写成如下形式：

Taylor 展开公式

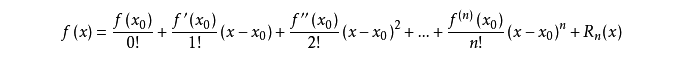
对于多元的函数展开，例如二元 f(x,y) 在坐标 (x0,y0) 处展开:

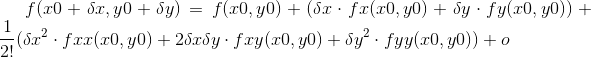
可以写成如下形式：

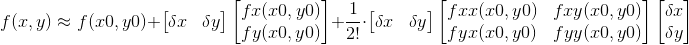
后面二阶导项可用海塞矩阵进行替换，而通常为了求得极值的必要条件是要得到一阶倒为0得点，可对上式两边进行求导

对比

两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法是用二阶的海森矩阵的逆矩阵求解。相对而言，使用牛顿法收敛更快（迭代更少次数）。但是每次迭代的时间比梯度下降法长。从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。通俗来说梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。

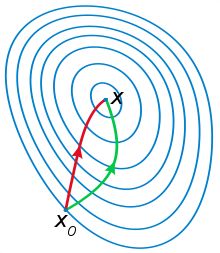
实际情况中，牛顿法中的Hesse Matrix的逆矩阵计算比较复杂，且消耗内存，故使用一些近似的矩阵来代替